问题
问答题
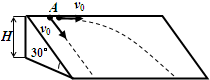
辨析题:如图所示,顶端高为H=0.8m的光滑斜面与水平面成θ=30°角.在斜面顶端A点处以大小为v=3m/s的速度,分别平行于斜面底边和垂直于斜面底边沿斜面抛出两个小球,使小球贴着斜面滑到斜面底端,试比较两个小球运动时间的长短.
有同学这样认为:两小球初速度大小相等,根据机械能守恒定律,两小球到达斜面底端的末速度大小也相等,所以平均速度相等,因此两小球运动的时间也相等.你认为这种观点正确吗?
如认为正确,请列式计算出小球运动时间.
如认为不正确,请列式计算比较两小球运动时间的长短.
答案

不正确.
斜面的长度为L=
=H sin30°
m=1.6m0.8 0.5
垂直于斜面底边沿斜面抛出的小球是A球,平行于斜面底边抛出的小球是B球,
根据机械能守恒定律
mv02+mgH=1 2
mvt21 2
得vt=
=v02+2gH
m/s=5m/s32+2×10×0.8
A球沿斜面做匀加速直线运动,tA=
=L v0+vt 2
s=0.4s1.6 3+5 2
对B球运动可以分解为沿初速度方向的匀速直线运动与垂直于初速度方向的初速度为零的匀加速运动
L=
gsinθ?tB21 2
tB=
=2L gsinθ
s=0.8s2×1.6 10×0.5
所以tA<tB
答:不正确.tA<tB.
