问题
多选题
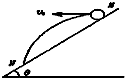
如图所示,从倾角为θ的斜面上的M点水平抛出一个小球,小球的初速度为v0,最后小球落在斜面上的N点,则( )
A.求出小球平抛运动过程的时间
B.不可能求出小球落到N点时速度的大小和方向
C.不可能求M、N之间的距离
D.可以断定,当小球速度方向与斜面平行时,小球与斜面间的距离最大
答案
设MN之间的距离为L,则由平抛运动的规律得
水平方向上:Lcosθ=V0t
竖直方向上:Lsinθ=
gt2 1 2
由以上两个方程可以解得 L=
,2
sinθV 20 gcos2θ
t=
V0tanθ,2 g
所以A正确,C错误,
B、在竖直方向上,由自由落体的速度公式可得在N点时竖直速度的大小,
Vy=gt=g?
V0tanθ=2V0tanθ,2 g
所以在N点时速度的大小为V=
=
+V 20 V 2y
,
+4V 20 V 20
θtan 2
夹角的正切值为 tanβ=
=2tanθ,Vy V0
所以B错误,
D、由物体的运动轨迹可以知道,物体离斜面的距离先变大在减小,当小球速度方向与斜面平行时,小球与斜面间的距离最大,所以D正确.
故选AD.
