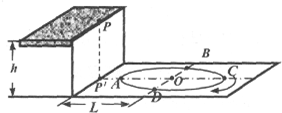
如图为一项体育娱乐节目示意图.水平地面上有一个半径为R的圆形跑道,A、B、C、D是跑道上的四个位置,O为跑道圆心,∠AOB=90°.高为h的平台边缘上的P点在地面P′点的正上方,P′、A、O、C在一直线上,P′与跑道圆心O的距离为L(L>R).跑道上停有一辆小车,选手可从P点向各个方向水平抛出小沙袋,使其落入小车中(沙袋所受空气阻力不计).问:
(1)当小车停于B点时,为使沙袋能落入小车中,沙袋被抛出时的初速度为多大?
(2)若小车在跑道上做匀速圆周运动(俯视图为顺时针方向),角速度ω=3π
.当小车运动到A点时,沙袋被抛出,为使沙袋能落入小车中,沙袋抛出时的初速度方向跟平台边缘的夹角为多大?g 2h
(1)当小车停于B点,为使沙袋能落入小车,则沙袋作平抛运动的水平距离为
x=
①L2+R2
又h=
gt2②1 2
x=v0t③
由以上①②③式得沙袋抛出时的水平速度v0=
.g(L2+R2) 2h
(2)沙袋落地前,小车做圆周运动转过的角度为θ=ωt④
由②、④两次得到θ=3π
可见,小车在沙袋刚好落地时运动到C点.
所以,沙袋被抛出时的初速度方向跟平台边缘的夹角为
.π 2
答:当小车停于B点时,为使沙袋能落入小车中,沙袋被抛出时的初速度为v0=
.g(L2+R2) 2h
(2)沙袋抛出时的初速度方向跟平台边缘的夹角为
.π 2