问题
选择题
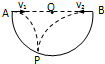
如图,半圆形凹槽的半径为R,O点为其圆心.在与O点等高的边缘A、B两点分别以速度v1、v2水平相向抛出两个小球,已知v1:v2=1:3,两小球恰落在弧面上的P点.则以下说法中正确的是( )
A.∠AOP为45°
B.若要使两小球落在P点右侧的弧面上同一点,则应使v1、v2都增大
C.改变v1、v2,只要两小球落在弧面上的同一点,v1与v2之和就不变
D.若只增大v1,两小球可在空中相遇
答案
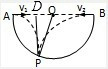
A、连接OP,过P点作AB的垂线,垂足为D,如图所示:
两球在竖直方向运动的位移相等,所以运动时间相等,
两球水平方向做运动直线运动,所以
=AD BD
=v1 v2 1 3
而AD+BD=2R
所以AD=
R1 2
所以OD=
R1 2
所以cos∠AOP=
=OD OP 1 2
即∠AOP=60°,故A错误;
B、若要使两小球落在P点右侧的弧面上同一点,则A球水平方向位移增大,B球水平位移减小,而两球运动时间相等,所以应使v1增大,v2减小,故B错误;

C、要两小球落在弧面上的同一点,则水平位移之和为2R,则(v1+v2)t=2R,落点不同,竖直方向位移就不同,t也不同,所以v1+v2也不是一个定值,故C错误;
D、若只增大v1,而v2不变,则两球运动轨迹如图所示,由图可知,两球必定在空中相遇,故D正确.
故选D
