问题
问答题
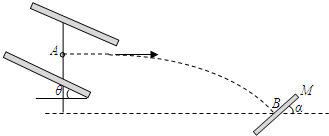
如图所示,板长为L的平行板电容器倾斜固定放置,极板与水平线夹角θ=30°,某时刻一质量为m,带电量为q的小球由正中央A点静止释放,小球离开电场时速度是水平的,(提示:离开的位置不一定是极板边缘)落到距离A点高度为h的水平面处的B点,B点放置一绝缘弹性平板M,当平板与水平夹角a=45°时,小球恰好沿原路返回A点.求:
(1)电容器极板间的电场强度E;
(2)平行板电容器的板长L;
(3)小球在AB间运动的周期T.
答案
(1)带电粒子沿水平方向做匀加速运动可知Eqcosθ=mg,
解得:E=
=mg qcosθ
.2
mg3 3q
(2)小球垂直落到弹性挡板上,且α=45°,
有v0=vy=2gh
根据动能定理:Eq?
Ltanθ=1 2
m1 2 v 20
解得:L=3h.
(3)由于小球在复合场中做匀加速运动
=L 2cosθ
gtanθ1 2 t 21
解得 t1=
=L gsinθ
,6h g
平抛运动的时间为 t2=
,2h g
总时间为 t=2t1+2t2=2(
+6h g
).2h g
答:(1)电容器极板间的电场强度E为
;2
mg3 3q
(2)平行板电容器的板长L为3h;
(3)小球在AB间运动的周期T为2(
+6h g
).2h g
