问题
问答题
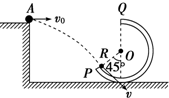
如图所示,竖直平面内有一光滑圆弧轨道,其半径为R,平台与轨道的最高点等高,一小球从平台边缘的A处水平射出,恰能沿圆弧轨道上的P点的切线方向进入轨道内侧,轨道半径OP与竖直线的夹角为45°,重力加速度为g,试求:
(1)小球从平台上的A点射出时的速度v0;
(2)小球从平台上射出点A到圆轨道入射点P之间的距离l;
(3)小球能否沿轨道通过圆弧的最高点?请说明理由.
答案
(1)小球从A到P的高度差h=R(1+cos45°)=(
+1)R2 2
小球做平抛运动有 h=
gt2 1 2
小球平抛时间 t=
=2h g (2+
)R2 g
则小球在P点的竖直分速度vy=gt=(2+
)gR2
把小球在P点的速度分解可得v0=vy
所以小球平抛初速度v0=(2+
)gR2
(2)小球平抛下降高度 h=
vy?t 1 2
水平射程 s=v0t=2h
故A、P间的距离
l=
=h2+s2
h 5
由上式可解得 l=(
+5 1 2
)R 10
(3)能.小球从A到达Q时,根据机械能守恒定律可得
vQ=v0=
>(2+
)gR2
,所以小球能通过圆弧轨道的最高点.gR
答:(1)小球从平台上的A点射出时的速度v0=
;(2+
)gR2
(2)小球从平台上射出点A到圆轨道入射点P之间的距离为
h;5
(3)小球能沿轨道通过圆弧的最高点,根据机械能守恒定律可得:vQ=v0=
>(2+
)gR2
,所以小球能通过圆弧轨道的最高点.gR
