问题
多选题
在倾角为30°高为h的斜面顶端,将一个小球沿水平方向抛出,抛出时小球的速度v=
,设小球在空中飞行到达某一位置的位移与水平方向的夹角α,速度与水平方向的夹角为β,则可能有( )2gh
A.一定是α<β
B.α>30°
C.β>30°
D.若使初速度v<
,小球落到斜面上时,其速度方向与斜面的夹角将不变2 3hg 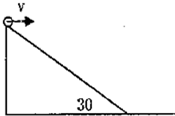
答案
A、位移与水平方向的夹角α的正切值为tanα=
=y x
=
gt21 2 v0t
,gt 2v0
速度与水平方向的夹角β的正切值为tanβ=
=vy v0
,gt v0
所以tanβ=2tanα,
所以一定是α<β,所以A正确;
BC、当小球落到地面上时,竖直方向上的速度最大,速度与水平方向的夹角也是最大的,
此时,小球的运动的时间为t,
由h=
gt2,可得1 2
t=
,2h g
所以此时的 tanβ=
=vy v0
=gt v0
=g 2h g 2gh
=1,2gh 2gh
所以小球在空中某位置时会有β>30°,所以C正确;
此时的tanα=
=y x
=h v0t
=h
?2gh 2h g
,1 2
所以α<30°,所以B错误;
D、当初速度v<
,小球落到斜面上时,
hg2 3
此时速度与水平方向的夹角β的正切值为tanβ=
=vy v0
=vyt v0t
,2y x
由于此时的小球落在斜面上,所以
=tan30°,y x
所以tanβ=2tan30°,
即速度与水平方向的夹角为定值,所以速度方向与斜面的夹角将不变,所以D正确.
故选ACD.
