问题
解答题
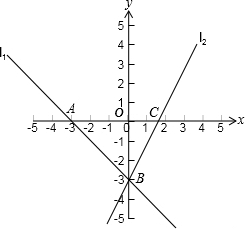
已知:直线l1、l2分别与x轴交于点A、C,且都经过y轴上一点B,又l1的解析式是y=-x-3,l2与x轴正半轴的夹角是60°.
求:(1)直线l2的函数表达式;
(2)△ABC的面积.
答案
(1)∵ℓ1:y=-x-3ℓ2与y轴交于同一点B
∴B(0,-3)又∵ℓ2与x轴正半轴的夹角是60°
∴∠MCx=60°即∠OCB=60°
在Rt△BOC中OB=3∴OC=B•tan30°=3×
=3 3 3
∴C(
,0)3
令ℓ:y=kx-3∴0=
k-3k=3 3
∴y=
x-33
(2)又∵ℓ1与x轴交于A,∴对于y=-x-3中当y=0时x=-3∴A(-3,0)
∴AC=
-(-3)=3+3
∴S△ABC=3
•(3+1 2
)×3=3 9+3 3 2