问题
选择题
如图所示,某物体自空间O点以水平初速度v0抛出,落在地面上的A点,其轨迹为一抛物线.现仿此抛物线制作一个光滑滑道并固定在与OA完全重合的位置上,然后将此物体从O点由静止释放,受微小扰动而沿此滑道滑下,在下滑过程中物体未脱离滑道.P为滑道上一点,OP连线与竖直成45°角,则此物体( )
A.由O运动到P点的时间为2 v0/g
B.物体经过P点时,速度的水平分量为2
v0/55
C.物体经过P点时,速度的竖直分量为v0
D.物体经过P点时的速度大小为22v0/5 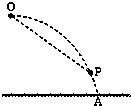
答案
A、物体若做平抛运动,有:v0t=
gt2,则t=1 2
.现在物体做的运动不是平抛运动,运动时间不等于2v0 g
.故A错误.2v0 g
B、物体若做平抛运动,运动到P点时竖直方向上的分速度vy=gt=2v0,此时速度与水平方向的夹角为α,则sinα=
=vy vy2+v02
.物块沿该轨道滑动,只有重力做功,根据动能定理得,mgh=2 5 5
mv2,解得v2=2gh=vy2,所以v=2v0.则物体经过P点时,速度的竖直分量vy′=2v0sinα=1 2
v0.速度的水平分量vx′=2v0cosα=4 5 5
.故B正确,C、D错误.2
v05 5
故选B.
