问题
多选题
如图所示，轮滑运动员从较高的弧形坡面上滑到A处时，沿水平方向飞离坡面，在空中划过一段抛物线后，再落到倾角为θ的斜坡上，若飞出时的速度大小为v0则（ ）
A．运动员落到斜坡上时，速度方向与坡面平行
B．运动员落回斜坡时的速度大小是V0 COSθ
C．运动员在空中经历的时间是2v0tanθ g
D．运动员的落点B与起飞点A的距离是2v20sinθ gcos2θ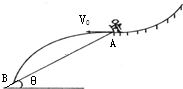 
答案
A、运动员落到斜坡上时，位移的方向与坡面平行，速度方向与坡面不平行．故A错误．
BCD、根据tanθ=
=y x
=
gt21 2 v0t
，解得t=gt 2v0
．则竖直方向上的分速度vy=gt=2v0tanθ，2v0tanθ g
所以落在斜坡上的速度v=
=v02+vy2
=v0v02+4v02tan2θ
．1+4tan2θ
水平位移x=v0t=
，则sAB=2v02tanθ g
=x cosθ
．故C、D正确，B错误．2v20sinθ gcos2θ
故选CD．