问题
问答题
设矩阵
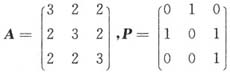，B=P-1A*P，其中A*是A的伴随矩阵，E为3阶单位矩阵
求B+2E的特征值与特征向量．
答案
参考答案：由于
[*]
故矩阵A的特征值为λ1=λ2=1，λ3=7．
当λ1=λ2=1时，由(E-A)x=0得到矩阵A的特征向量为
α1=(-1，1，0)T，α2=(-1，0，1)T
当λ3=7时，由(7E-A)x=0得到矩阵A的特征向量为
α3=(1，1，1)T．
如果 Aα=λα有[*]，那么
[*]
进而 [*]
又[*]
所以 B+2E的特征值为9，9，3．
矩阵B+2E对应于λ=9的特征向量是
[*]，其中k1，k2为任意非零常数．
对应于λ=3的特征向量是
[*]，k3为任意非零常数．
