问题
问答题
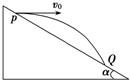
如图所示,宇航员站在某质量分布均匀的星球表面一斜坡上P点沿水平方向以初速度v0抛出一个小球,测得小球经时间t落到斜坡上另一点Q,斜面的倾角为α,已知该星球半径为R,万有引力常量为G,求:
(1)该星球表面的重力加速度;
(2)该星球的密度;
(3)该星球的第一宇宙速度v;
(4)人造卫星绕该星球表面做匀速圆周运动的最小周期T.
答案
(1)设该星球表现的重力加速度为g,根据平抛运动规律:
水平方向:x=v0t
竖直方向:y=
gt21 2
平抛位移与水平方向的夹角的正切值tanα=
=y x
gt21 2 v0t
得g=
; 2v0tanα t
(2)在星球表面有:G
=mg,所以M=Mm R2 gR2 G
该星球的密度:ρ=
; 3v0tanα 2πRtG
(3)由
=mGMm R2
,可得v=v2 R
,GM R
又GM=gR2,所以v=
; 2v0Rtanα t
(4)绕星球表面运行的卫星具有最小的周期,即:
T=
=2πR2πR v t 2v0Rtanα
故答案为:(1)g=
;(2)该星球的密度ρ=2v0tanα t
;(3)该星球的第一宇宙速度v=3v0tanα 2πRtG
;(4)人造卫星绕该星球表面做匀速圆周运动的最小周期2πR2v0Rtanα t t 2v0Rtanα
