问题
问答题
设随机变量X与Y相互独立，X的概率分布为PX=i=
(i=-1，0，1)，Y的概率密度为
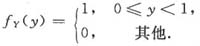记Z=X+Y．
求Z的概率密度fZ(z)．
答案
参考答案：FZ(z)=P{Z≤z}-P{X+Y≤z}．可以把“X=-1”，“X=0”和“X=1”看成是一个完备事件组，用全概率公式：
[*]
故
[*]
即
[*]
搜题请搜索小程序“爱下问搜题”
设随机变量X与Y相互独立，X的概率分布为PX=i=
(i=-1，0，1)，Y的概率密度为
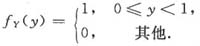记Z=X+Y．
求Z的概率密度fZ(z)．
参考答案：FZ(z)=P{Z≤z}-P{X+Y≤z}．可以把“X=-1”，“X=0”和“X=1”看成是一个完备事件组，用全概率公式：
[*]
故
[*]
即
[*]