问题
问答题
设f(x)是周期为2的连续函数.
证明对任意实数,有
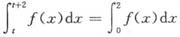 ;
;
答案
参考答案:[证法一] 由f(x)是周期为2的连续函数知,[*]在(-∞,+∞)上可导,且
F’(t)=f(t+2)-f(t)=0 ([*]t∈(-∞,+∞))
[*] F(t)=常数=F(0)
即
[*]
[证法二] 利用定积分的性质考察
[*]
[*]
因此
[*]
设f(x)是周期为2的连续函数.
证明对任意实数,有
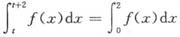 ;
;
参考答案:[证法一] 由f(x)是周期为2的连续函数知,[*]在(-∞,+∞)上可导,且
F’(t)=f(t+2)-f(t)=0 ([*]t∈(-∞,+∞))
[*] F(t)=常数=F(0)
即
[*]
[证法二] 利用定积分的性质考察
[*]
[*]
因此
[*]