如图所示，半径r=0.3m、质量M的光滑14圆弧面放在光滑的水平长桌

问题问答题

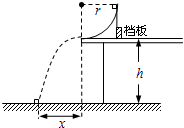
如图所示，半径r=0.3m、质量M的光滑

圆弧面放在光滑的水平长桌面上，桌面离地面高h=0.8m．将一质量为m小物体从圆弧最高处静止释放，为了防止圆弧面在桌面上的滑动，在圆弧面右侧固定了档板．若两物体的质量满足M=2m．求：

（1）小物体由静止释放后，小物体的水平射程x．

（2）小物体由静止释放后，落地时速度的大小．

（3）某次操作中忘记安装档板，发现小物体静止释放后，圆弧面开始向右运动，最后测得小物体的水平射程x₀=0.8m，则小物体滑离后圆弧面在桌面上运动的最大速度v_M．

答案

（1）设小物体到达圆弧底端速度v，则下滑的过程中由动能定理得mgr=

mv2…①

小物体做平抛运动，有：

gt2…②

x=vt…③

由上述列式得x≈0.98m

（2）由机械能守恒可知：mg(r+h)=

mv′2

由上述列式得v′=

2g(r+h)

2×10×(0.3+0.8)

m/s；

（3）小物体离开圆弧面后，圆弧面速度最大，设小物体离开桌面速度v₁，圆弧面速度v₂．

小物体做平抛运动，有：

gt2

x₀=v₁t

小球下滑中和圆弧面整体用动能定理，有：mgr=

得v₂=1 m/s

答：（1）小物体由静止释放后，小物体的水平射程x为0.98m；

（2）小物体由静止释放后，落地时速度的大小为

m/s；

（3）小物体滑离后圆弧面在桌面上运动的最大速度为1m/s．