问题
问答题
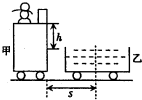
如图所示,甲、乙两车静止在光滑水平面上.人静止站立在甲车上,乙车装满砂.已知甲车和人的总质量等于乙车和砂的总质量,均为M,两车高度差为h,甲车右端与乙车中点相距s,在甲车右端另放一质量为m且与甲车无摩擦力的物体,若人将物体向右踢出,使物体恰好落在乙车的中点.不计物体陷入砂中的深度,且人相对于甲车始终静止.求:
(1)乙车最终的速度.
(2)人做了多少功?
答案
(1)设m飞出速度为v1,人和甲车速度为v2,对m平抛过程有
s=v1t,h=
gt21 2
联立解得,v1=sg 2h
m与乙车作用过程,设作用后共同速度为v,水平方向动量守恒,则有
mv1=(m+M)v
联立得:v=ms M+m g 2h
(2)人踢开物体m的过程,由动量守恒得:
Mv2=mv1
由功能关系得:W=
m1 2
+v 21
M1 2 v 22
联立得:W=m(M+m)gs2 4Mh
答:(1)乙车最终的速度是ms M+m
.g 2h
(2)人做功为
.m(M+m)gs2 4Mh
