问题
解答题
已知∠AOB、∠A′O′B′且AO∥A′O′,BO∥B′O′,猜想∠AOB与∠A′O′B′有怎样的数量关系?请说明理由,由本题你可以得到什么样的结论?(用一句话叙述)
答案
解:∠AOB=∠A′O′B′或∠AOB+∠A′O′B′=180°;
如图(1),
∵OA∥O′A′(已知),
∴∠O=∠A′CB(两直线平行,同位角相等),
又∵OB∥O′B′,
∴∠A′CB=∠O′(两直线平行,同位角相等),
∴∠O=∠O′,即∠AOB=∠A′O′B′;
如图(2),
∵OA∥O′A′,
∴∠O=∠OCO′(两直线平行,内错角相等),
又∵OB∥O′B′,
∴∠OCO′+∠B′O′C=180°(两直线平行,同旁内角互补),
∴∠AOB+∠A′O′B′=180°。
结果:如果两角、两边分别平行,则两角相等或互补。
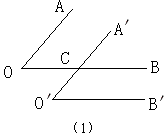

问答题 案例分析题
