如图所示，水平屋顶高H=5m，围墙高h=3.2m，围墙到房子的水平距离

问题问答题

如图所示，水平屋顶高H=5m，围墙高h=3.2m，围墙到房子的水平距离L=3m，围墙外马路宽x=10m，为使小球从屋顶水平飞出落在围墙外的马路上，求小球离开屋顶时的速度v的大小范围．（g取10m/s²）

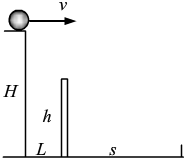
答案

若v太大，小球落在马路外边，因此，球落在马路上，v的最大值v_max为球落在马路最右侧A点时的平抛初速度，

如图所示，小球做平抛运动，设运动时间为t₁．

则小球的水平位移：L+x=v_maxt₁，

小球的竖直位移：H=

解以上两式得

v_max=（L+x）

=13 m/s．

若v太小，小球被墙挡住，因此，

球不能落在马路上，v的最小值v_min

为球恰好越过围墙的最高点P落在马路上B点时的平抛初速度，

设小球运动到P点所需时间为t₂，

则此过程中小球的水平位移：L=v_mint₂

小球的竖直方向位移：H-h=

解以上两式得v_min=L

2(H-h)

=5 m/s

因此v₀的范围是v_min≤v≤v_max，

即5 m/s≤v≤13 m/s．

答：小球离开屋顶时的速度v的大小范围5 m/s≤v≤13 m/s．