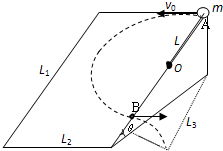
如图所示,一个长L1=0.9m、宽L2=0.6m的光滑斜面体,其倾角θ=30°.有一长度L=0.4m的轻质绳一端固定在距斜面顶点A为L=0.4m斜面边缘的O点上,另一端系一质量m=1kg的小球.现把小球拉至顶点A处,以v0=1m/s的初速度沿斜面顶边缘水平抛出.(g取10m/s2)
(1)刚开始小球做什么运动?并说明理由.
(2)求小球运动至斜面边缘B点时受到绳子的拉力FT.
(3)若小球运动至B点时绳子刚好断了,求小球从斜面上飞出后落地点与最初抛出点在地面上投影点的距离L3.
(1)小球沿斜面向下的加速度a=
=5m/s2mgsinθ m
其在斜面上运动可等效看作在g′=a=5m/s2的竖直平面上的曲线运动
由于小球刚抛出的速度v0<
=g′L
m/s,故其开始做类平抛运动.2
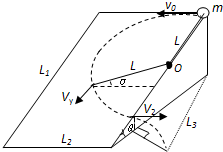
(2)如图所示,设它运动时间t秒至与水平线的夹角为α时,绳子刚好拉直.由平抛运动公式有:
L+Lsinα=
g′t 2①1 2
Lcosα=v0t②
①②联立并代入数据解得:α=0°,t=0.4s
α=0°,说明小球抛至绳子在水平线时刚好拉直.在拉直瞬间,由于绳子不可伸长,故小球水平速度瞬间变为零,只存在沿斜面向下的速度vy
vy=g′t=5×0.4m/s=2m/s
以后小球在绳子束缚下沿斜面向下做圆周运动,设至B点时的速度为v2.根据机械能守恒定律,有:
mg′L+
mvy2=1 2
mv221 2
代入数据解得:v2=
m/s8
根据牛顿第二定律,有:F T-mg′=mv 2 2 L
代入数据解得:FT=25N
(3)绳断后小球以v2做平抛运动,由题意知其高度h′=0.05m,设至落地所需时间为t′,
根据h=
gt′ 2解得:t′=0.1s,水平位移x=v2t′1 2
而本题斜面有效长度在地面投影长度L4=v2t′=0.4
m3
所求的距离L 3=
=x 2+L 4 2
m(或≈0.75m)0.56
答:
(1)刚开始小球做类平抛运动.
(2)小球运动至斜面边缘B点时受到绳子的拉力FT=25N.
(3)若小球运动至B点时绳子刚好断了,小球从斜面上飞出后落地点与最初抛出点在地面上投影点的距离L3≈0.75m.
