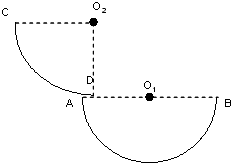
如图所示,AB是固定在竖直平面内半径为R的光滑半圆弧,CD是与AB在同一竖直平面内半径为1.5R的四分之一光滑圆弧轨道,其底端D切线水平,且与AB弧圆心O1等高.现将质量为m的小球(可视为质点)从圆弧CD上与圆心O2等高的C处由静止开始释放,小球落进半圆弧AB并与之内壁碰撞,碰撞过程中不损失机械能,结果小球刚好能回到D点并能沿DC弧返回C处.g=10m/s2.求:
(1)小球刚滑倒D点时,对D段的压力大小
(2)CD弧底端D距AB弧圆心O1的距离
(3)小球与圆弧AB的内壁碰撞时的速度大小.
(1)设小球滑到D点速度为v,从C滑到D的过程,由机械能守恒定律有:
mv2=1.5mgR,得v=1 2 3gR
在D点,由牛顿第二定律有:F-mg=m
,v2 1.5R
联立发上两式解得:F=3mg,
所以小球对D段的压力大小F′=F=3mg,方向竖直向下;
(2)小球欲回到D点,与弧面的碰撞必须是垂直弧面的碰撞,即速度方向沿弧AB的半径方向.设碰撞点和O1的连线与水平夹角α,D点和碰撞点连线与水平夹角为β,则有
x=vt,y=
gt21 2
vy=gt,vx=v
tanα=vy v
y=Rsinα,
解得:sinα=
,得α=30°,vy=1 2
,x=gR
R,3
D到O1的距离为:DO1=x-Rcosα=
R;3 2
(3)小球与圆弧AB的内壁碰撞时的速度大小v′=
=2vy sinα
.gR
答:
(1)小球刚滑倒D点时,对D段的压力大小为3mg.
(2)CD弧底端D距AB弧圆心O1的距离为
R.3 2
(3)小球与圆弧AB的内壁碰撞时的速度大小是2
.gR
