问题
问答题
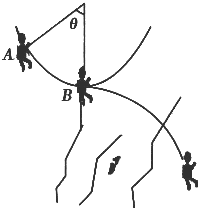
某实验中学的学习小组在进行科学探测时,一位同学利用绳索顺利跨越了一道山涧,他先用绳索做了一个单摆(秋千),通过摆动,使自身获得足够大的速度后再平抛到山涧对面,如图所示,若他的质量是M,所用绳长为L,在摆到最低点B处时的速度为v,离地高度为h,当地重力加速度为g.
(1)他用的绳子能承受的最大拉力应不小于多少?
(2)这道山涧的宽度不超过多大?
(3)若该同学是从某高处A点无初速度下摆的,则下摆时绳子倾角θ为多大?
答案
(1)该同学在B处,由牛顿第二定律得,
F-Mg=Mv2 L
解得F=Mg+M
.v2 L
即他用的绳子能承受的最大拉力应不小于Mg+M
.v2 L
(2)该同学做平抛运动的过程中由运动学公式得,水平方向上有:x=vt
竖直方向上有h=
gt21 2
解得x=v
,即这道山涧的宽度不超过v2h g
.2h g
(3)对该同学从A处下摆到B处的过程由动能定理得,
Mg(L-Lcosθ)=
Mv2-01 2
解得θ=arccos(1-
).v2 2gL
答:(1)用的绳子能承受的最大拉力应不小于Mg+M
.v2 L
(2)这道山涧的宽度不超过v
.2h g
(3)下摆时绳子倾角θ为θ=arccos(1-
).v2 2gL
