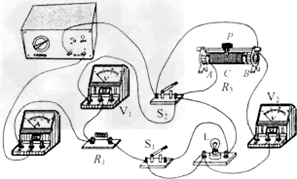
如图所示的电路中,电源两端电压不变,设灯L电阻不变.当开关S1闭合,S2断开,滑动变阻器的滑片P移到B端时,R1的电功率为P1,电流表示数为I1;当开关S1断开,S2闭合时,R1的电功率为P1′,电流表示数为I2,此时灯L正常发光.当开关S1、S2都断开,滑动变阻器的滑片P在C点时,变阻器接入电路的电阻为Rc,电压表V1的示数为U1,电压表V2的示数为U1,已知U1:U2=3:2,Rc的电功率为18W,P1:P1′=9:25.电路通过断开、闭合开关以及滑动变阻器滑片P的移动,形成不同电路所消耗的最大电功率与最小电功率之比为3:1.求:
(1)电流I1与I2的比值;
(2)灯的电阻R1与R1的比值;
(3)灯L正常发光2min所消耗电能W的大小.(请画出相关电路状态的等效电路图)
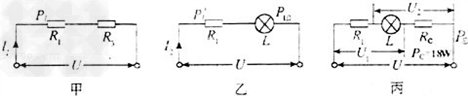
解:当S1闭合、S2断开,滑片P在B端时,电路如图甲所示;
当S1断开、S2闭合时,灯正常发光,电路如图乙所示;
当S1、S2都断开,滑片P在C时,电路如图丙所示.
(1)如图甲、乙:
∵ 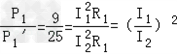 ,
,
∴ .
.
(2)当S1和S2都断开,滑片P在B端时,电路如图(A),
总电阻最大,总功率Pmin;
当S1和S2都闭合时,电路如图(B),
总电阻最小,总功率Pmax.

∵ U一定, ∴ 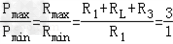 ,
,
∴2R1=RL+R3①,
∴ 如图甲、乙,U一定,
∴ 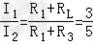 ,
,
∴ 2R1=3R3﹣5RL②,
解①②式得:3RL=R3,R1=2RL,
∴ 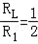 .
.
(3)如图丙: ∴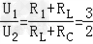 ,
,
∴2R1=RL+3RC③,
将R1=2RL,代入③式,
解得:RC=RL,
∴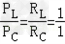 ,
,
∴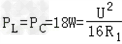 ,
,
如图乙,灯正常发光:∵ 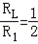 ,
,
∴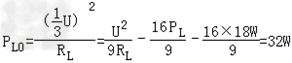 ,
,
∴ WL0=PL0t=32W×2×60s=3840J.
