问题
问答题
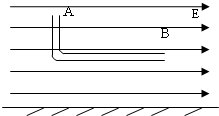
如图所示,水平地面上方分布着水平向右的匀强电场.一“L”形的绝缘硬质管竖直固定在匀强电场中.管的水平部分长为l1=0.2m,离水平地面的距离为h=5.0m,竖直部分长为l2=0.1m.一带正电的小球从管的上端口A由静止释放,小球与管间摩擦不计且小球通过管的弯曲部分(长度极短可不计)时没有能量损失,小球在电场中受到的静电力大小为重力的一半,求:
(1)小球运动到管口B时的速度大小;
(2)小球着地点与管的下端口B的水平距离.(g=10m/s2).
答案
(1)在小球从A运动到B的过程中,对小球由动能定理有:
mvB2-0=mgl2+F电l1,①1 2
由于小球在电场中受到的静电力大小为重力的一半,即 F电=
mg ②1 2
代入数据可得:vB=2.0m/s③
小球运动到管口B时的速度大小为2.0m/s.
(2)小球离开B点后,设水平方向的加速度为a,位移为s,在空中运动的时间为t,
水平方向有:a=
,④g 2
s=vBt+
at2,⑤1 2
竖直方向有:h=
gt2,⑥1 2
由③~⑥式,并代入数据可得:s=4.5m.
故小球着地点与管的下端口B的水平距离为4.5m.
