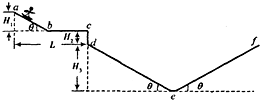
滑板运动是一项陆地上的“冲浪运动”,具有很强的观赏性.如图所示,abcdef为同一竖直平面内的滑行轨道,其中bc段水平,ab、de和ef段均为倾角θ=37°的斜直轨道,轨道间均用小圆弧平滑相连(小圆弧的长度可忽略).已知H1=5m,L=15m,H2=1.25m,H3=12.75m,设滑板与轨道之间的摩擦力为它们间压力的k倍(k=0.25),运动员连同滑板的总质量m=60kg.运动员从a点由静止开始下滑从c点水平飞出,在de上着陆后,经短暂的缓冲动作后保留沿斜面方向的分速度下滑,接着在def轨道上来回滑行,除缓冲外运动员连同滑板可视为质点,忽略空气阻力,取g=10m/s2,sin37°=0.6,cos37°=0.8.求:
(1)运动员从c点水平飞出时的速度大小vc;
(2)运动员在de上着陆时,沿斜面方向的分速度大小v0;
(3)设运动员第一次和第四次滑上ef轨道时上升的最大高度分别为h1和h4,则h1:h4等于多少?
(1)设运动员从a点到c点的过程中克服阻力做功Wf,
根据动能定理得:
mgH1-Wf=
m1 2
-0①v 2c
而Wf=kmgcosθ•
+kmg•. ab
②. bc
L=abcosθ+
③. bc
由①②③式并代入数据,解得vc=5m/s④
(2)运动员从c点水平飞出到落到de轨道上的过程中做平抛运动,设从c点到着陆点经过的时间为t
水平位移x=vxt⑤
竖直位移y=
gt2⑥1 2
由几何关系
=tanθ⑦y-H2 x
水平方向分速度vx=vc⑧
竖直方向分速度vy=gt⑨
v0=vxcosθ+vysinθ⑩
由④⑤⑥⑦⑧⑨⑩式并代入数据,解得v0=10m/s
(3)设运动员第一次沿ed斜面向上滑的最大高度为h1',
根据功能关系mg(h1-
)=kmgcosθ(h ′1
+h1 sinθ
)h ′1 sinθ
解得
=h ′1
h11 2
同理可得,运动员第二次沿ef斜面向上滑的最大高度h2=1 2
=(h ′1
)2h11 2
以此类推,运动员第四次沿ef斜面向上滑的最大高度h4=(
)6h11 2
解得
=h4 h1 1 64
答:(1)运动员从c点水平飞出时的速度大小vc为5m/s;
(2)运动员在de上着陆时,沿斜面方向的分速度大小v0为10m/s;
(3)设运动员第一次和第四次滑上ef轨道时上升的最大高度分别为h1和h4,则h1:h4等于1:64.
