问题
问答题
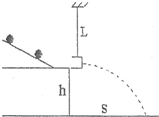
利用如图所示的方法测定细线的抗拉强度.在长为L的细线下端悬挂一只质量不计的小盒,小盒的左侧开一孔,一个金属小球从斜轨道上释放后,水平进入小盒内,与小盒一起向右摆动.现逐渐提高金属小球在轨道上释放的高度,直至摆动时细线恰好被拉断,并测得此时金属小球平抛运动的竖直位移h和水平位移S,若小球质量为m,试求该细线的抗拉断张力多大?
答案
小球做平抛运动,有:
h=
gt21 2
S=v0t
在金属盒中,重力和拉力的合力提供向心力,根据牛顿第二定律,有:
T-mg=mv 20 L
联立解得:
T=mg(1+
)S2 2hL
答:该细线的抗拉断张力为mg(1+
).S2 2hL
