如图所示,一个固定在竖直平面内的轨道,有倾角为θ=37°的斜面AB和水平面BC以及另一个倾角仍为θ=37°的斜面DE三部分组成.已知水平面BC长为0.4m,D位置在C点的正下方,CD高为H=0.9m,E点与C点等高,P为斜面DE的中点;小球与接触面间的动摩擦因数均为μ=0.15,重力加速度g取10m/s2.现将此小球离BC水平面400h高处的斜面上静止释放,小球刚好能落到P点(sin37°=0.6,cos37°=0.8).
(1)求h的大小;
(2)若改变小球在斜面上静止释放的位置问小球能否垂直打到斜面DE上的Q点(CQ⊥DE).若能,请求出h的大小;若不能,请说明理由?
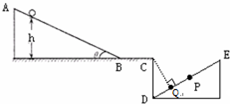
(1)研究小球从C点到P点的平抛过程
竖直位移y=
=0.45mH 2
水平位移x=
cot370=0.6mH 2
在竖直方向上,可求得t=
=0.3s2y g
在水平方向上,初速度vC=
=2m/sx t
小球从静止开始运动直到C点的过程中,由动能定理:
mgh-μmgcos370×
-μmgSBC=h sin370
m1 2 v 2C
解得:
h=0.325m
(2)小球不可能垂直打到Q点;
理由:若小球在斜面上的落点位置为Q点,则OQ为小球运动的位移,且在Q点与斜面垂直,由速度角与位移角关系,速度与水平方向夹角必大于位移与水平方向偏角,故小球不可能垂直打到Q点;(或理由:假设小球可以垂直打到Q点,则在Q点的速度方向的反向延长线必指向C点,由于运动轨迹为抛物线,则抛出点在C点下方,与题意不符.)
答:(1)释放点的高度h的大小为0.325m;
(2)小球不能垂直打到斜面DE上的Q点,理由为:若小球在斜面上的落点位置为Q点,则OQ为小球运动的位移,且在Q点与斜面垂直,由速度角与位移角关系,速度与水平方向夹角必大于位移与水平方向偏角,故小球不可能垂直打到Q点.

 安抚
安抚