问题
问答题
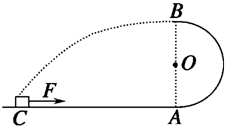
如图所示,半径R=0.4m的光滑半圆轨道与粗糙的水平面相切于A点,质量为m=1kg的小物体(可视为质点)在水平拉力F的作用下,从静止开始由C点运动到A点,物体从A点进入半圆轨道的同时撤去外力F,物体沿半圆轨道通过最高点B后做平抛运动,正好落在C点,已知xAC=2m,F=15N,g取10m/s2,试求:
(1)物体在B点时的速度大小以及此时半圆轨道对物体的弹力大小;
(2)物体从C到A的过程中,摩擦力做的功.
答案
(1)设物体在B点的速度为v,由B到C做平抛运动,
竖直方向有:2R=
gt21 2
水平方向有:xAC=vt
∴联立以上两式解得物体在B点时的速度大小为:v=
=XAC t
=XAC 4R g
m/s=5 m/s2 4×0.4 10
分析物体在B点的受力由牛顿第二定律得:FN+mg=mv2 R
∴解得半圆轨道对物体的弹力大小为:FN=
-mg=mv2 R
N-1×10N=52.5 N1×52 0.4
(2)A到B过程,由机械能守恒定律得:
mvA2=1 2
mv2+2mgR1 2
由C到A应用动能定理可知:(F-Ff)xAC=
mvA21 2
所以,联立以上两式解得物体从C到A的过程中摩擦力做的功为:Wf=-Ff•xAC=
mVA2FXAC=1 2
×1×41J-15×2J=-9.5 J.1 2
答案:(1)5 m/s 52.5 N (2)-9.5 J
