问题
问答题
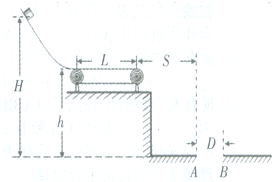
光滑曲面的末端与一长L=1m的水平传送带相切,传送带离地面的高度h=1.25m,地面上有一个直径D=0.5m的圆形洞,洞口最左端的A点离传送带右端的水平距离S=1m,B点在洞口的最右端,传动轮作顺时针转动,使传送带以恒定的速度运动,现使某小物体(可看做质点)从曲面上距离地面高度H处由静止开始释放,刚到达传送带上时小物体的速度恰好和传送带相同,并最终恰好由A点落入洞中.已知小物体与传送带间动摩擦因数μ=0.1,g取10m/s2.
求:
(1)传送带的运动速度v的大小;
(2)H的大小.
答案
(1)物体滑上传送带后与传送带一起做匀速直线运动,平抛运动的初速度等于传送带的速度.
由h=
gt2得,1 2
t=
=2h g
s=0.5s2×1.25 10
v=
=s t
m/s=2m/s1 0.5
故传送带的速度为2m/s.
(2)根据动能定理得,mg(H-h)=
mv2-01 2
代入数据得,H=1.45m.
故H的大小为1.45m.
