问题
问答题
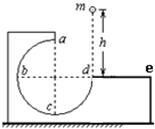
如图所示,固定在水平桌面上的有缺口的方形木块,abcd为半径为R(已知量)的四分之三圆周的光滑轨道,a为轨道的最高点,de面水平且有足够长度.今将质量为m的小球在d点的正上方某一高度为h(未知量)处由静止释放,让其自由下落到d处切入轨道内运动,小球恰能通过a点,(不计空气阻力,已知重力加速度为g)求:
(1)小球恰能通过a点时的速度.(用已知量R及g表示)
(2)小球通过a点后最终落在de面上的落点距d的水平距离.
答案
(1)小球恰能通过a点的条件是小球的重力提供向心力,
根据牛顿第二定律:mg=mv2 R
解得:v=gR
(2)小球离开a点时做平抛运动,用平抛运动的规律,
水平方向的匀速直线运动:x=vt
竖直方向的自由落体运动:R=
gt2,1 2
解得:x=
R2
所以落地距d点的距离为:x-R=(
-1)R2
答:
(1)小球恰能通过a点时的速度为
,(2)小球通过a点后最终落在de面上的落点距d的水平距离为(gR
-1)R2
