问题
问答题
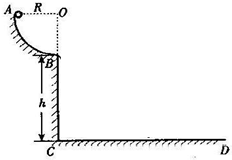
如图所示,轨道ABCD的AB段为一半径R=0.2m的光滑1/4圆形轨道,BC段为高为h=5m的竖直轨道,CD段为水平轨道.一质量为0.1kg的小球由A点从静止开始下滑到B点时速度的大小为2m/s,离开B点做平抛运动(g=10m/s2),求:
(1)小球运动到B点时的向心加速度
(2)小球离开B点后,在CD轨道上的落地点到C的水平距离;
(3)小球到达B点时对圆形轨道的压力大小?
答案
(1)小球做圆周运动,
则由an=v2 r
解得:an=
m/s2=20m/s222 0.2
(2)小球做平抛运动,由平抛运动规律得
竖直方向h=
gt2 1 2
水平方向x=vt
解得:x=2m.
(3)小球B点受力分析,则有重力,支持力.
所以F向=F-G=mv2 R
解得F=3N
由牛顿第三定律知球对B的压力F′=F,即小球到达B点时对圆形轨道的压力大小为3N,方向竖直向下.
答:(1)小球运动到B点时的向心加速度20m/s2;
(2)小球离开B点后,在CD轨道上的落地点到C的水平距离2m;
(3)小球到达B点时对圆形轨道的压力大小3N.
