物体做圆周运动时，所需的向心力F需由运动情况决定，提供的向心

问题问答题

物体做圆周运动时，所需的向心力F_需由运动情况决定，提供的向心力F_供由受力情况决定．若某时刻F_需=F_供，则物体能做圆周运动；若F_需＞F_供，物体将做离心运动；若F_需＜F_供，物体将做向心运动．现有一根长L=1m的刚性轻绳，其一端固定于O点，另一端系着质量m=0.5kg的小球（可视为质点），将小球提至正上方的A 点处，此时绳刚好伸直且无张力，如图所示．不计空气阻力，g取10m/s²，则：

（1）为保证小球能在竖直面内做完整的圆周运动，在A点至少应施加给小球多大的水平速度？

（2）若小球以速度v₁=4m/s水平抛出的瞬间，绳中的张力为多少？

（3）若小球以速度v₂=1m/s水平抛出的瞬间，绳中若有张力，求其大小？若无张力，试求绳子再次伸直时所经历的时间？

答案

（1）要使小球在竖直面内能够做完整的圆周运动，在最高点时至少应该是重力作为所需要的向心力，

所以由 mg=m

得

V₀=

m/s，

（2）因为v₁＞V₀，故绳中有张力，

由牛顿第二定律得，

T+mg=m

代入数据解得，绳中的张力为T=3N，

（3）因为v₂＜V₀，故绳中没有张力，小球将做平抛运动，如图所示

水平方向：x=v₂t

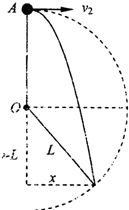
竖直方向：y=

gt²

L²=（y-L）²+x²

解得：t=

gl-

=0.6s．

答：（1）在A点至少应施加给小球

m/s 的水平速度；

（2）若小球以速度v₁=4m/s水平抛出的瞬间，绳中的张力为3N；

（3）若小球以速度v₂=1m/s水平抛出的瞬间，绳中无张力，绳子再次伸直时所经历的时间是0.6s．