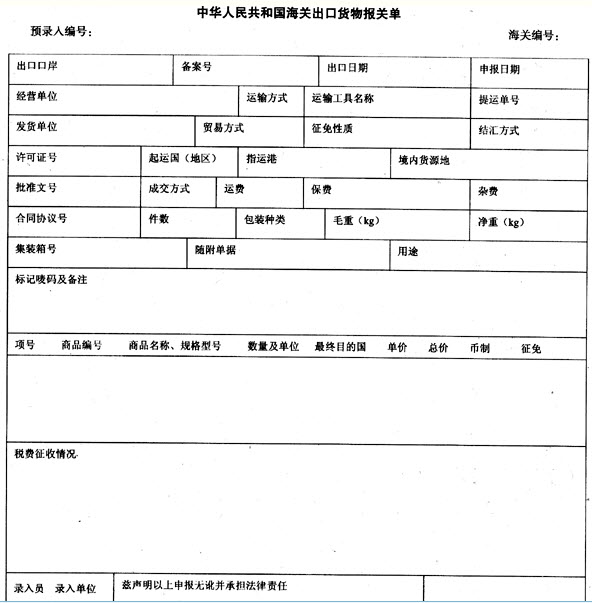
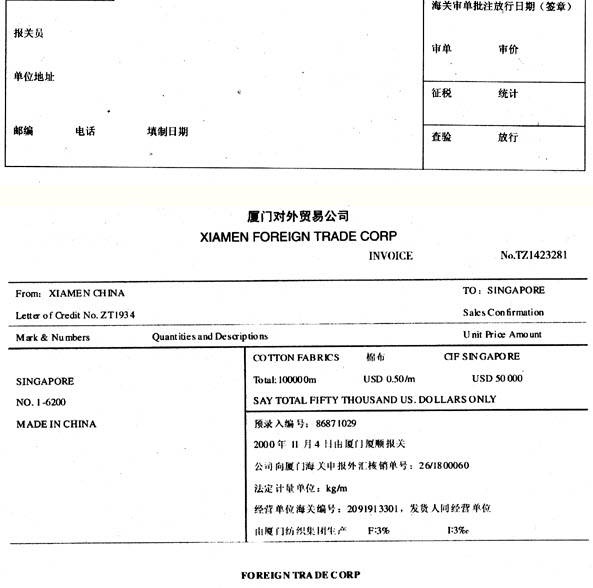
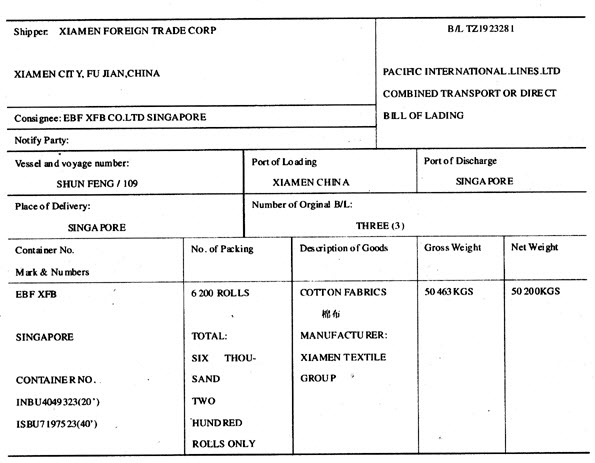
问题
解答题
设x,y,z,w为四个互不相等的实数,并且x+
求证:x2y2z2w2=1 |
答案
证明:∵x+
=y+1 y
=z+1 z
=w+1 ω 1 x
∴
⇒x+
=y+1 y 1 z y+
=z+1 z 1 ω z+
=ω+1 ω 1 x ω+
=x+1 x 1 y
⇒x-y=
-1 z 1 y y-z=
-1 ω 1 z z-ω=
+1 x 1 ω ω-x=
-1 y 1 y (x-y)zy=y-z ① (y-z)ωz=z-ω ② (z-ω)xω=ω-x ③ (ω-x)yx=x-y ④
由①×②×③×④得,x2y2z2w2(x-y)(y-z)(z-w)(w-x)=(x-y)(y-z)(z-w)(w-x)
∵x,y,z,w互不相等
∴x2y2z2w2=1.