问题
问答题
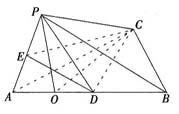
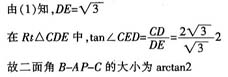如图，在三棱锥P-ABC中，∠APB=90°，∠PAB=60°，AB=BC=CA，平面PAB⊥平面ABC。
（1）求直线PC与平面ABC所成角的大小；
（2）求二面角B-AP-C的大小。
答案
参考答案：
(1)设AB的中点为D，AD的中点为O，连接PO、CO、CD，由已知，△PAD为等边三角形，
所以PO⊥AD
又平面PAB⊥平面ABC，平面PAB∩平面ABC=AD，
所以PO⊥平面ABC
所以∠OCP为直线PC与平面ABC所成的角
(2)过D作DE⊥AP于E，连接CE
由已知可得，CD⊥平面PAB
根据三垂线定理知，CD⊥PA
所以∠CED为二面角B-AP-C的平面角
