问题
问答题
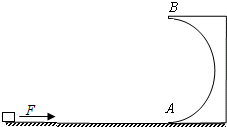
半径为R=0.9m的光滑半圆形轨道固定在水平地面上,与水平面相切于A点,在距离A点1.3m处有一可视为质点的小滑块,质量为m=0.5kg,小滑块与水平面间的动摩擦因数为μ=0.2,施加一个大小为F=11N的水平推力,运动到A点撤去推力,滑块从圆轨道最低点A处冲上竖直轨道.(g=10m/s2)问:
(1)滑块在B处对轨道的压力;
(2)滑块通过B点后的落地点到B点的水平距离.
答案
(1)从开始到B点的过程由动能定理得:
mvB2-0=Fx-μmgx-mg•2R1 2
代入数据解得:vB=4m/s
对滑块在B点受力分析,受重力和轨道对滑块的压力,由牛顿第二定律:
FN+mg=mv 2B R
解得:FN=3.9N
根据牛顿第三定律知道轨道对小球的压力滑块在B处对轨道的压力大小相等,方向相反
所以滑块在B处对轨道的压力大小为3.9N,方向竖直向上.
(2)离开B点做平抛运动:z
竖直方向:2R=
gt2 1 2
水平方向:x=vt
解得:x=2.4m
答:(1)滑块在B处对轨道的压力大小为3.9N,方向竖直向上.;
(2)滑块通过B点后的落地点到B点的水平距离为2.4m.
