如图所示，固定的四分之一竖直圆弧轨道AB的半径R=0.6m，其最低点

问题问答题

如图所示，固定的四分之一竖直圆弧轨道AB的半径R=0.6m，其最低点与长L=2．Om、高h=0.2m、质量M=5．Okg的长木板的水平上表面相切于B点．质量 m=1.0kg的小滑块（可视为质点）从圆弧顶点A处由静止释放，当它运动到圆弧最低点B时受轨道的支持力为25N．已知滑块与长木板间的动摩擦因数μ₁=0.2，长木板与水平地面间的动摩擦因数

μ₂=0.1，g取10m/s²．求：

（1）滑块由A运动到B的过程中，阻力对它做的功．

（2）滑块在长木板上运动的时间．

（3）滑块落地时的速度大小．

答案

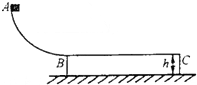
（1）滑块滑到B点时，根据向心力公式得：

F_N-mg=m

vB2

解得：v_B=3m/s

滑块从A到B的过程运用动能定理得：

mgR+W_f=

mvB2

解得：W_f=-1.5J

（2）长木板受到滑块对它的摩擦力为f₁=μ₁mg=2N

长木板受到地面对它的摩擦力为f₂=μ₂（M+m）g=6N

因为f₁＜f₂，故长木板不动．

滑块在长木板上运动的加速度大小为a=

=2m/s²

设滑块在长木板上运动的时间为t，则

L=v_Bt-

at2

解得t=1s

（3）滑块运动到C点的速度为v_C=v_B-at=1m/s

滑块离开木板后做平抛运动，设其竖直方向速度为v_y则：

vy2=2gh

vC2+vy2

m/s

答：（1）滑块由A运动到B的过程中，阻力对它做的功为-1.5J；（2）滑块在长木板上运动的时间为1s；（3）滑块落地时的速度大小

m/s．