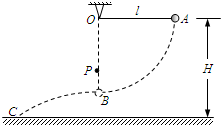
一长l=0.80m的轻绳一端固定在O点,另一端连接一质量m=0.10kg的小球,悬点O距离水平地面的高度H=1.00m.开始时小球处于A点,此时轻绳拉直处于水平方向上,如图所示.让小球从静止释放,当小球运动到B点时,轻绳碰到悬点O正下方一个固定的钉子P时立刻断裂.绳断裂后球从B点抛出并落在水平地面的C点,不计轻绳断裂的能量损失,取重力加速度g=10m/s2.
(1)求小球到达B点时的速度.
(2)求C点与B点之间的水平距离.
(3)若轻绳所能承受的最大拉力Fm=9.0N,求钉子P与O点的距离d应满足什么条件?
(1)从A到B的过程中,小球的机械能守恒,由机械能守恒定律可得,
mgH=mg(H-l)+
mV2,1 2
解得 V=4m/s,
(2)从C到B的过程中,小球做平抛运动,
水平方向上:x=Vt
竖直方向上:h=
gt21 2
其中的V=4m/s,h=0.2m,
代入数据求得 x=0.8m,
(3)对小球受力分析,绳的拉力和重力的合力作为合力提供向心力,
所以F-mg=m
,V2 r
解得r=0.2m,
所以钉子P与O点的距离至少为 d=l-r=0.8m-0.2m=0.6m,
答:(1)小球到达B点时的速度是4m/s.
(2)C点与B点之间的水平距离为0.8m.
(3)钉子P与O点的距离d应大于或等于0.6m.
