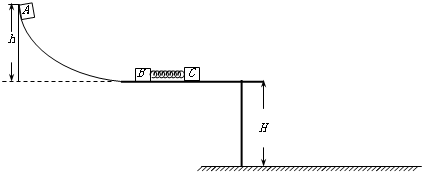
如图所示,一轻质弹簧的一端固定在滑块B上,另一端与滑块C接触但未连接,该整体静止放在离地面高为H=5m的光滑水平桌面上.现有一滑块A从光滑曲面上离桌面h=1.8m高处由静止开始滑下,与滑块B发生碰撞并粘在一起压缩弹簧推动滑块C向前运动,经一段时间,滑块C脱离弹簧,继续在水平桌面上匀速运动一段后从桌面边缘飞出.已知mA=1kg,mB=2kg,mC=3kg,g=10m/s2,求:
(1)滑块A与滑块B碰撞结束瞬间的速度;
(2)被压缩弹簧的最大弹性势能;
(3)滑块C落地点与桌面边缘的水平距离.
(1)滑块A从光滑曲面上h高处由静止开始滑下的过程,机械能守恒,设其滑到底面的速度为v1,
由机械能守恒定律有:mAgh=
mA1 2 v 21
解得:v1=6m/s
滑块A与B碰撞的过程,A、B系统的动量守恒,碰撞结束瞬间具有共同速度设为v2,
由动量守恒定律有:mAv1=(mA+mB)v2
解得:v2=
v1=2m/s1 3
(2)滑块A、B发生碰撞后与滑块C一起压缩弹簧,压缩的过程机械能守恒,被压缩弹簧的弹性势能最大时,滑块A、B、C速度相等,设为速度v3,v3=
v1=1m/s1 6
由动量守恒定律有:mAv1=(mA+mB+mC)v3
由机械能守恒定律有:Ep=
(mA+mB)v22-1 2
(mA+mB+mC)v321 2
Ep=3J
(3)被压缩弹簧再次恢复自然长度时,滑块C脱离弹簧,设滑块A、B的速度为v4,滑块C的速度为v5,
分别由动量守恒定律和机械能守恒定律有:
(mA+mB)v2=(mA+mB)v4+mCv5
(mA+mB)1 2
=v 22
(mA+mB)1 2
+v 24
mC1 2 v 25
解得:v4=0,
V5=2m/s
滑块C从桌面边缘飞出后做平抛运动:
gt2S=v5t1 2
H=
gt21 2
解得:S=2m
答:(1)滑块A与滑块B碰撞结束瞬间的速度是2m/s;
(2)被压缩弹簧的最大弹性势能是3J;
(3)滑块C落地点与桌面边缘的水平距离为2m.
