问题
问答题
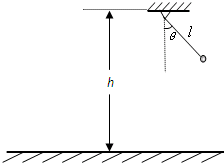
如图所示,用一根长l为0.8m的细绳,一端拴一个质量为m的小球,另一端悬于离地面高h为2.6m处,当细绳受到3mg拉力时会被拉断,现把这小球拉到使细绳与竖直方向夹角为θ时由静止释放,若球摆到细绳竖直位置时,绳子刚好被拉断,小球平抛落到地面.求:
(1)小球摆到细绳竖直位置时速度大小?
(2)小球落地点离绳子断裂位置的水平距.
答案
(1)小球摆到细绳竖直位置时,由重力和细绳的拉力的合力提供小球的向心力,由牛顿第二定律得:
T-mg=mv2 l
又由题知:T=3mg
联立解得:v=
=2gl
m/s=4m/s2×10×0.8
(2)绳子断裂后,小球做平抛运动,初速度为v=4m/s.则
竖直方向:h-l=
gt2,1 2
得:t=
=2(h-l) g
s=0.6s2×(2.6-0.8) 10
水平方向:x=vt=4×0.6m=2.4m
答:(1)小球摆到细绳竖直位置时速度大小是4m/s.
(2)小球落地点离绳子断裂位置的水平距离是2.4m.
