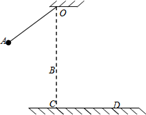
如图所示,质量为m=5kg的摆球从图中A位置由静止开始摆下,当小球摆至竖直位置到达B点时绳子恰好被拉断.已知摆线长为L=1.6m,OA与OB的夹角为60°,悬点O与地面间的距离hOC=4m,若不计空气阻力及一切能量损耗,g=10m/s2,求:
(1)小球摆到B点时的速度大小;
(2)小球落地点D到C点之间的距离;
(3)若选用不同长度的绳子进行实验,仍然保证OA与OB的夹角为60°,且绳子在处于竖直方向时拉断,为了使小球的落点D与C之间的距离最远,请通过计算求绳子的长度和CD间最远距离.
(1)设小球摆到B点的速度为v,由动能定理得
mgL(1-cosθ)=
mv21 2
得到 v=
=4m/s2gL(1-cosθ)
(2)小球从B点飞出后,做平抛运动,平抛的时间为t,
则有h-L=
gt21 2
水平方向,小球做匀速直线运动,则有x=vt
故CD间的距离为 x=vt=4×0.8=3.2m
(3)设绳子长度为l,则由前两问可得CD间的距离
x=vt=
•2gl(1-cosθ)
=2(h-l) g 2l(h-l)
由均值定理可得,当l=h-l即l=2.4m时,x有最大值
代入即可得x=3.4m.
答:(1)小球摆到B点时的速度大小0 4m/s;
(2)小球落地点D到C点之间的距离为3.2m;
(3)绳长为2.4m时,CD间距离最远,为3.4m.
