问题
问答题
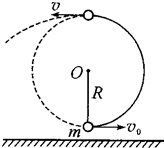
如图所示,长为R的不可伸长轻绳上端固定在O点,下端连接一只小球,小球与地面间的距离可以忽略(但小球不受地面支持力)且处于静止状态.现给小球一沿水平方向的初速度,
使其开始在竖直平面内做圆周运动.设小球到达最高点时轻绳突然断开,已知最后小球落在距初始位置水平距离为4R的地面上,重力加速度为g.试求:(图中所标初速度v0的数值未知)
(1)绳突然断开时小球的速度;
(2)小球刚开始运动时对绳的拉力.
答案
(1)绳突然断开后,小球做平抛运动,竖直方向做自由落体运动,由h=
gt2得:t=1 2
=2h g
,4R g
小球水平方向做匀速直线运动,由x=vt得:v=
=x t
=24R 4R g
;gR
(2)在小球从最低点运动到最高点的过程中运用动能定理得:
mv2-1 2
mv02=-mg•2R,1 2
解得:v0=8gR
小球在最低点做圆周运动,根据FN=m
得:v2 r
T-mg=mv02 R
解得:T=9mg.
根基牛顿第三定律可知,球对绳的拉力为9mg.
1)绳突然断开时小球的速度为2
;(2)小球刚开始运动时对绳的拉力为9mg.gR
