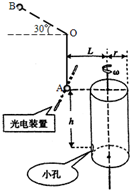
如图所示，一根长l=0.8m轻绳一端固定在O点，另一端栓一质量m=0.1

问题问答题

如图所示，一根长l=0.8m轻绳一端固定在O点，另一端栓一质量m=0.1kg的小球静止于A点，其右方有底面半径r=0.2m的转筒，转筒顶端与A等高，下部有一小孔，距顶端h=0.8m．现使细绳处于水平线上方30°的位置B点处而伸直，且与转筒的轴线、OA在同一竖直平面内，开始时小孔也在这一竖直平面内．将小球由B点静止释放，当小球经过A点时轻绳突然断掉，同时触动了光电装置，使转筒立刻以某一角速度匀速转动起来，且小球最终正好进入小孔．不计空气阻力，g取l0m/s²．

（1）辨析题：求小球到达A点时的速率？

某同学解法如下：小球从B点运动到A点过程中，只有重力做功，故机械能守恒，则mgl(1+sin30°)=

mvA2，代入数据，即可求得小球到达A点时的速率．

你认为上述分析是否正确？如果你认为正确，请完成此题；如果你认为不正确，请指出错误，并给出正确的解答．

（2）求转筒轴线距A点的距离L

（3）求转筒转动的角速度ω

答案

（1）此同学解法不正确．设细绳到C位置断掉．

从B→C过程：根据机械能守恒得：mgl=

小球在C点切向速度为 v_C切=v_Csin60°

从C到A，只有重力做功，据机械能守恒定律得

mgl(1-cos60°)+

2C切

解得，vA=2

m/s

（2）滑块从A点到进入小孔的时间为

2×0.8

s=0.4s

又由题意得 L-r=v_A•t

得 L=

m=1.99m

（3）在小球平抛的时间内，圆桶必须恰好转整数转，小球才能钻入小孔

即ωt=2nπ（n=1，2，3…）

解得，ω=5nπ（rad/s）（n=1，2，3…）

答：

（1）此同学解法不正确．小球到达A点时的速率为2

m/s．

（2）转筒轴线距A点的距离L是1.99m

（3）转筒转动的角速度ω是5nπ（rad/s）（n=1，2，3…）