问题
问答题
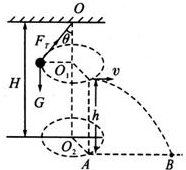
如图所示,能承受最大拉力Fm=10N的细线长L=0.6m,它的一端固定于高H=2.1m的O点,另一端系一质量为m=0.5kg的小球在水平面内做圆周运动,由于转速加快而使细线断裂.求:小球落地点距O点的水平距离是多大?(g取10m/s2)
答案
(1)小球在水平面内做圆周运动时,由重力G和拉力F的合力提供向心力,
设绳将要断时,绳与竖直方向的夹角为θ,
由竖直方向小球受力平衡有
cosθ=
=G Fm
=0.5×10 10
,1 2
所以,θ=60°
由几何关系得:小球做圆周运动的半径为
R=Lsinθ=0.6×
m=3 2
m.3 3 10
当绳断时,沿半径方向,牛顿第二定律得:
mg•tanθ=
,mv2 R
解得:v=
=gR•tan60°
m/s=3m/s.10×0.3×
×3 3
(2)绳断后,小球做平抛运动,这时小球离地面的高度h为
h=H-Lcos60°=(2.1-0.6×
)m=1.8m.1 2
由平抛规律h=
gt2,求得小球做平抛运动的时间1 2
t=
=2h g
s=0.6s.2×1.8 10
水平位移 x=vt=3×0.6m=1.8m.
小球落地点距O2的距离为:
=. O2B
=x2+R2
m1.82+(0.3×
)23
=
m≈1.87m. 3.51
答:小球落地点距O点的水平距离为1.87m.
