问题
问答题
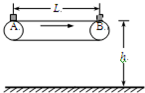
如图为车站使用的水平传送带装置的示意图,绷紧的传送带始终保持8.0m/s的恒定速率运行,传送带的水平部分AB距水平地面的高度h=0.45m,现有一质量为m=10kg的行李包(可视为质点)从静止开始由A端被传送到B端,且传送到B端时没有被及时取下,行李包从B端水平抛出.已知行李包与传送带之间动摩擦因数为μ=0.2,且A与B之间距离为L=9m.不计空气阻力,g取10m/s2.
(1)行李包从A传送到B的过程中,摩擦力对物块做的功为多少?
(2)行李包从B端水平抛出后落地点到B点的水平距离?
答案
(1)以行李包为研究对象,
由牛顿第二定律得:μmg=ma,a=2m/s2,
由匀变速运动的速度位移公式得:v2-0=2ax,解得,
行李包速度等于8m/s时的位移x=16m>L=9m,
则行李包速度没有达到8m/s时离开传送带,
摩擦力对行李包做的功W=μmgL=0.2×10×10×9=180J;
(2)由匀变速运动的速度位移公式得:vB2-0=2aL,
行李包到达B端的速度vB=6m/s,
行李包离开传送带后做平抛运动,
在竖直方向:h=
gt2,1 2
在水平方向:x=vBt,
解得:x=1.8m;
答:(1)行李包从A传送到B的过程中,摩擦力对物块做的功为6m/s.
(2)行李包从B端水平抛出后落地点到B点的水平距离为1.8m.
