问题
问答题
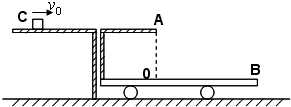
如图所示,在光滑的水平面上停着一辆小车,小车平台的上表面是粗糙的.它靠在光滑的水平桌面旁并与桌面等高.现在有一个质量为m=2kg的物体C以速度v0=10m/s沿水平桌面向右运动,滑过小车平台后从A点离开,恰能落在小车前端的B点.已知小车总质量为M=5kg,O点在A点的正下方,OA=0.8m,OB=1.2m,物体与小车摩擦系数µ=0.2,g取10m/s2.
求:(1)物体刚离开平台时,小车获得的速度大小.
(2)物体在小车平台上运动的过程中,小车对地发生多大的位移.
答案
(1)设物体C刚离开小车平台时,速度为v1.此时小车速度为v2,C从A点落到B点的时间为t,
由动量守恒定律,得mv0=mv1+Mv2…①
C从A点落到B点做平抛运动,由平抛运动规律,
有OA=
gt2…②1 2
OB=v1t-v2t…③
由①②③解得:v1=5m/s
(2)设C滑上平台到离开平台所需时间为t',在平台上,物体C和小车的加速度分别为
a1=
=2m/s2(方向:水平向左)μmg m a2=
=0.8m/s2(方向:水平向右)μmg M
则t′=
=2.5sv0-v1 a1
故小车对地位移为:s=
a2t′2=1 2
×0.8×2.52m=2.5m1 2
答:(1)物体刚离开平台时,小车获得的速度大小为5m/s.
(2)物体在小车平台上运动的过程中,小车对地发生多大的位移为2.5m.