问题
问答题
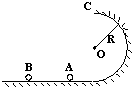
如图所示,半径为R的光滑半圆轨道竖直放置,两个质量均为m的小球A、B以不同的速率进入轨道,A通过最高点C时,对轨道的压力为3mg,B通过最高点C时,对轨道的压力恰好为零,求:
(1)A、B两球从C点飞出的速度分别为多少?
(2)A、B两球落地点间的距离.
答案
(1)以A为研究对象,在最高点时,则有:
FN+mg=mv 2A R
FN=3mg
解得:vA=2gR
以B为研究对象,在最高点时,则有:
mg=mv 2B R
解得:vB=gR
(2)两球从C点飞出后都做平抛运动
竖直方向:2R=
gt21 2
得:t=2R g
水平方向:
xA=vAt
xB=vBt
A、B两球落地点间的距离:△x=xA-xB
代入解得:△x=2R
答:
(1)A、B两球从C点飞出的速度分别为2
和gR
.gR
(2)A、B两球落地点间的距离为2R.
