问题
问答题
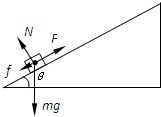
半径R=4500km的某星球上有一倾角为θ=30°的固定斜面.一质量为m=1lg的小物块在力F作用下从静止开始沿斜面向上运动,力F始终与斜面平行,如图12(甲)所示.已知小物块和斜面间的动摩擦因数μ=
,力F随位移s变化的规律如图(乙)所示(取沿斜面向上的方向为正),那么小物块运动12m时速度恰好为零.试求:3 3
(1)该星球表面上的重力加速度;
(2)该星球表面抛出一个物体,为使该物体不再落回星球,至少需要多大速度?

答案
(1)假设星球表面的重力加速度为g,根据动能定理:
小物块在力F1作用过程中有:
F1s1-fs1-mgs1sinθ=
mv2-01 2
又 f=μN=μmgcosθ
小物块在力F2作用过程中有:
-F2s2-fs2-mgs2sinθ=0-
mv21 2
由图可知:F1=20N,s1=6m,F2=4N,s2=6m
由①②③式得:g=8m/s2
(2)要使抛出的物体不再落回星球,物体的最小速度V,必须满足:
mg=mV2 R
得到 V=
=6.0km/sgR
答:(1)该星球表面上的重力加速度为8m/s2;
(2)该星球表面抛出一个物体,为使该物体不再落回星球,至少需要6.0km/s速度.
