问题
问答题
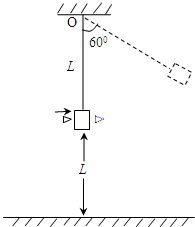
如图所示,质量为M的小沙箱,被长为L的细绳静悬于距离地面高L的空中.一质量为m的子弹水平射向沙箱:子弹与沙箱相互作用的时间极短;子弹从沙箱穿出时速度方向未改变,落地点距悬点O的水平位移为2
L;沙箱摆动的最大角度为60°,沙箱尺寸远小于L.不计空气阻力,已知M=8m,试求2
(1)子弹射出沙箱的瞬间,沙箱的速率和细绳对沙箱拉力的大小;
(2)射出沙箱后的瞬间与射入沙箱前的瞬间,子弹速率分别是多少.
答案
(1)设子弹射出沙箱的瞬间,沙箱的速率为v箱,则
MgL(1-cos60°)=
M1 2 v 2箱
解得 v箱=gL
又根据牛顿第二定律得
T-Mg=Mv 2箱 L
解得T=2Mg=16mg
(2)设子弹射出沙箱的瞬间,速率为为v子,
则L=
gt2 1 2
2
L=v子t2
解得v子=2gL
由动量守恒得:
mv0=mv子+Mv箱
解得v0=M+2m m
=10gL gL
答:(1)子弹射出沙箱的瞬间,沙箱的速率和细绳对沙箱拉力的大小16mg;
(2)射出沙箱后的瞬间与射入沙箱前的瞬间,子弹速率分别是2
和10gL
.gL
