如图所示，一小球自平台上水平抛出，恰好落在临 * * 台的一倾

问题问答题

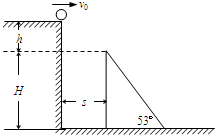
如图所示，一小球自平台上水平抛出，恰好落在临 * * 台的一倾角为α=53°的光滑斜面顶端，且速度方向与斜面平行，小球沿斜面下滑，已知斜面的顶点与平台的高度差h=0.80m（取g=10m/s²，sin53°=0.60，cos53°=0.80）求：

（1）小球水平抛出的初速度v₀；

（2）斜面顶端与平台边缘的水平距离s；

（3）若斜面顶端高H=1.95m，小球到达地面时的速率．

答案

（1）由题意可知：小球落到斜面上并沿斜面下滑，说明此时小球速度方向与斜面平行，否则小球会弹起，所以

v_y=v₀tan53°

v_y²=2gh

代入数据，得v_y=4m/s，v₀=3m/s

故小球的水平速度为3m/s；

（2）由v_y=gt₁得t₁=0.4s

s=v₀t₁=3×0.4m=1.2m

（3）小球落到斜面上时的速度v=

v02+vy2

=5m/s．

根据动能定理得，mgH=

mv′2-

mv2

解得v′=8m/s．

答：（1）小球的水平初速度为3m/s；

（2）水平距离为1.2m．

（3）小球到达地面时的速率8m/s．