问题
问答题
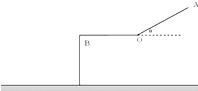
滑雪运动员从A点由静止沿倾角为 θ 的斜面滑下,经一平台后水平飞离B点,B点离地高度为 H,斜面、平台与滑雪板之间的动摩擦因数均为 μ.OA=OB=L,假设滑雪者由斜面底端进入平台后立即沿水平方向运动,且速度大小不变.求:
(1)滑雪者在斜面上的加速度的大小.
(2)滑雪者离开 B 点时的速度大小.
(3)滑雪者的落地点与 B 点的水平距离.
答案
(1)滑雪者在斜面上滑动过程,对运动员受力分析,受重力、支持力和滑动摩擦力,
根据牛顿第二定律,有:mgsinθ-μmgcosθ=ma;
解得:a=g(sinθ-μcosθ);
(2)A到B的过程,由动能定理得
mgLsinθ-μmgcosθL-μmgL=
mv2;1 2
解得:v=
;2gL(sinθ-μcosθ-μ)
故滑雪者离开B点时的速度为
;2gL(sinθ-μcosθ-μ)
(3)雪者离开B点到着地过程,只受重力,是平抛运动,根据平抛运动的分位移公式,有:
x=vt
H=
gt21 2
联立解得:x=2
;HL(sinθ-μcosθ-μ)
答:(1)滑雪者在斜面上的加速度的大小为g(sinθ-μcosθ).
(2)滑雪者离开B点时的速度大小为
.2gL(sinθ-μcosθ-μ)
(3)滑雪者的落地点与 B 点的水平距离为2
.HL(sinθ-μcosθ-μ)
