如图,在xOy坐标中第Ⅰ和第Ⅳ象限中分布着平行于x轴的匀强电场,第Ⅳ象限的长方形OPQH区域内还分布着垂直坐标平面的、大小可以任意调节的匀强磁场.一质子从y轴上的a点射入场区,然后垂直x轴通过b点,最后从y轴上的c点离开场区.已知:质子质量为m、带电量为q,射入场区时的速率为v0,通过b点时的速率为v0,=2=2d,==d
(1)在图中标出电场和磁场的方向;
(2)求:电场强度E的大小以及c到坐标原点的距离;
(3)如果撤去电场,质子仍以v0从a点垂直y轴射入场区.试讨论质子可以从长方形OPQH区域的哪几条边界射出场区,并求从这几条边界射出时对应磁感应强度B的大小范围和质子转过的圆心角θ的范围.
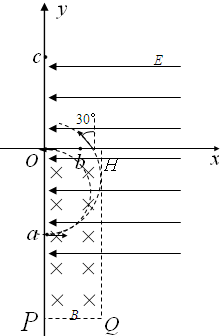
(1)质子从a到b洛伦兹力不做功,只有电场力做功,由于动能减少,电场力做负功,所以电场沿x轴负方向.依题意质子的运动轨迹从a到b,根据曲线运动的条件和左手定则可判断磁场方向垂直纸面向里.故电场方向指向x轴负方向;磁场方向垂直纸面向里.
(2)质子从a到b,洛伦兹力不做功,仅电场力做功.由动能定理得:
-qE•=-qE•=m•(v0)2-m…①
得:E=…②
质子从b到c,做类平抛运动,设运动时间为t,
则:=v0t…③
=at2=t2…④
联立②、③、④得:=d…⑤
(3)质子在磁场中,洛伦兹力提供向心力,设做圆周运动的半径R,则
qBv0=…⑥
即:R=⑦
讨论:
(i)如图,当R>=d时,质子将从HQ边射出,此时:0<B<,0<θ< ⑧
(ii)当=d≥R≥=d时,质子将从OH边射出,此时:≤B≤,π≥θ≥π⑨
(iii)当R<=d时,质子将从Oa边射出,此时:B>,θ=π⑩
答:(1)电场方向指向x轴负方向;磁场方向垂直纸面向里.
(2)电场强度E的大小为,c到坐标原点的距离等于d;
(3)(i)当R>=d时,质子将从HQ边射出,此时:0<B<,0<θ<.
(ii)当=d≥R≥=d时,质子将从OH边射出,此时:≤B≤,π≥θ≥π.
(iii)当R<=d时,质子将从Oa边射出,此时:B>,θ=π.


